Logical bitwise (bitwise) operations Bitwise shift operations
In the last article we discussed the topic of logical operations and expressions. In this article we will look at logical bit operations . Bit operations are very close to logical operations, one might even say that they are one and the same. The only difference is that logical operations are applied to statements, and bit operations, with the same rules and results, are applied to bits.
Bit operations play an important role in the program; they make it easier and more practical to implement the programmer’s plans.
Therefore, there is no need to be afraid of the expression “bit operations” and of them themselves, especially since what is scary and incomprehensible about them is only in the name. And I will try to tell you as much as possible about bit operations and their application in the practice of programmers. A number of sources on low-level languages call bitwise logical operations simply logical, but in the terminology of programming in high-level languages, the names of bitwise operations contain the adjectives bitwise, bitwise, bitwise. In common programming languages, only four bitwise logical operations are implemented by built-in means: AND, OR, NOT and exclusive OR. To specify an arbitrary bitwise logical operation, the listed operations are sufficient.
So that we do not get confused with the expressions “bit operation” and “bit operation”, remember that performing a bit operation is performing bit operations on individual bits, and in the future I will simply write “bit operation” or “logical operation”.
In addition, while reading technical literature, you will probably come across the terms “unary operation” and “binary operation”. A unary operation is an operation on one operand (Bitwise operation “NOT”). Binary operation - an operation with two operands (Bit operations “AND”, “OR”, “EXCLUSIVE OR”)
And also, I will denote the general-purpose register (R0...R31) with the abbreviation RON.
Why do we need bitwise operators?
In the distant past, computer memory was very scarce and highly valued. This was an incentive to use every available bit as wisely as possible. For example, in the boolean data type bool there are only two possible values (true and false), which can be represented by one bit, but in fact take up an entire byte of memory! And this, in turn, is due to the fact that variables use unique memory addresses, and they are allocated only in bytes. The bool variable takes up 1 bit and the other 7 bits are wasted.
Using bitwise operators, you can create functions that will allow you to fit 8 bool values into a 1-byte variable, which will significantly save memory consumption. This trick was very popular in the past. But today, at least in application programming, this is not the case.
Now there is significantly more memory and programmers have discovered that it is better to write code in such a way that it is easier and clearer to maintain, rather than complicating it for the sake of insignificant memory savings. Therefore, the demand for using bitwise operators has decreased somewhat, except in cases where maximum optimization is necessary (for example, scientific programs that use huge amounts of data; games, where bit manipulation can be used for additional speed; embedded programs, where memory is limited). still limited).
There are 6 bitwise operators in C++:
| Operator | Symbol | Example | Operation |
| Bitwise shift left | << | x << y | All bits in x are shifted left by y bits |
| Bitwise shift right | >> | x >> y | All bits in x are shifted to the right by y bits |
| Bitwise NOT | ~ | ~x | All bits in x are reversed |
| Bitwise AND | & | x&y | Every bit in x And every corresponding bit in y |
| Bitwise OR | | | x | y | Each bit in x OR each corresponding bit in y |
| Bitwise exclusive OR (XOR) | x^y | Each bit in x XOR with each corresponding bit in y |
In bitwise operations, you should use only integer data types , since C++ does not always guarantee that bitwise operators will work correctly with signed integer types.
Rule: When working with bitwise operators, use unsigned .
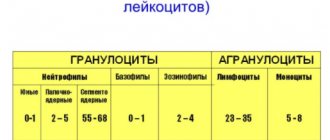
Leukogram
The leukogram or leukocyte formula is the ratio of the absolute and relative number of white blood cells. Their quantity is determined simultaneously with red blood cells, platelets, hemoglobin level and color index, and is included in a general blood test, as well as an immunogram.
A shift in the leukocyte formula to the left implies an increase in the number of young and immature forms of neutrophils, the appearance of reticulocytes, metamyelocytes and myelocytes in the peripheral bloodstream. This picture may indicate a compensatory state after blood loss, an inflammatory reaction, bone marrow damage, or radiation sickness. Therefore, in addition to a blood test, it is important to do a complete examination.
A shift of the leukogram to the right is an increase in the absolute and relative number of “obsolete” neutrophils (segmented). This blood behavior indicates anemia, diseases of parenchymal organs, as well as a compensatory window after transfusion of blood components.
Bitwise shift left (<<) and bitwise shift right (>>)
In C++, the number of bits used is based on the size of the data type (there are 8 bits in 1 byte). The bitwise left shift operator (<<) shifts bits to the left. The left operand is the expression in which they are shifted, and the right one is the number of places to shift. So in the expression 3 << 1 we mean “shift the bits to the left in the literal 3 by one place.”
Note: In the following examples we will work with 4-bit binary values.
Consider the number 3, which in binary is equal to 0011:
3 = 0011 3 << 1 = 0110 = 6 3 << 2 = 1100 = 12 3 << 3 = 1000 = 8
In the last third case, one bit moves beyond the literal itself! Bits shifted outside of the binary number are lost forever.
The bitwise right shift operator (>>) shifts bits to the right. For example:
12 = 1100 12 >> 1 = 0110 = 6 12 >> 2 = 0011 = 3 12 >> 3 = 0001 = 1
In the third case, we again moved the bit outside the literal. He is also lost forever.
Although in the examples above we are only shifting bits in literals, we can also shift bits in variables:
| 1 2 | unsigned int x = 4; x = x << 1; // x should become equal to 8 |
It should be remembered that the results of bitwise shift operations may differ between compilers.
Leukocyte formula - what is it?
The leukocyte formula is the ratio of the number of certain types of leukocytes (there are five in total) to the total number of these blood cells. A shift in proportion indicates that an infection has entered the body, there is inflammation, a purulent process has begun, or another pathology is present. This is what shifts the leukocyte formula. Types of leukocytes (they are also called white cells or bodies):
- Neutrophils. Has an antimicrobial effect.
- Monocytes. Promote tissue restoration, destroy foreign bodies, and participate in the formation of the immune response.
- Eosinophils. Appear after the body is damaged by infection. This is a response to a stimulus.
- Lymphocytes. They participate in the destruction of foreign bodies, forming protective antibodies.
- Basophils. Promote the movement of other leukocytes to sites of infection.
Having studied the change in the normal number of cells, the doctor makes a preliminary diagnosis and prescribes the necessary additional examinations.
Bitwise NOT operator
The bitwise NOT operator (~) is perhaps the easiest to explain and understand. It simply reverses each bit, such as 0 to 1 or 1 to 0. Note that the results of bitwise do NOT depend on the size of the data type!
Let's assume the size of the data type is 4 bits:
4 = 0100 ~ 4 = 1011 (binary) = 11 (decimal)
Let's assume the data type size is 8 bits:
4 = 0000 0100 ~ 4 = 1111 1011 (binary) = 251 (decimal)
Counting methods
In order to determine whether there is a shift in the leukocyte formula to the left, universal methods for counting blood cells are needed. They should be simple and accessible to any laboratory, because a clinical blood test is basic in any medical study.
Blood cells are distributed unevenly on the glass slide, as they have different densities:
- the peripheral position is occupied by neutrophils, basophils and eosinophils;
- Monocytes and lymphocytes are located closer to the center of the glass.
To count the number of leukocytes, two methods are most often used - Schilling and Filipchenko.
The Schilling method involves determining the number of cells in four opposite areas on a glass slide. In total there are about one hundred or two hundred cells. Based on this quantity, the ratio between the fractions is calculated.
Filipchenko’s method involves the laboratory assistant mentally dividing the smear into three parts:
- initial;
- average;
- final
Cells are counted along a conventional line drawn across the smear. In each part, the same number of cells is counted. The total is about two hundred leukocytes. All cells are recorded in a table or Egorov grid. In order to quickly and accurately determine the leukocyte formula, in addition to the differential table, a special 11-key calculator is used.
Bitwise operators AND, OR and exclusive OR (XOR)
The bitwise AND (&) and OR (|) operators work similarly to AND and OR operators However, bitwise operators are applied to each bit separately! For example, consider the expression 5 | 6. In binary it is 0101 | 0110. In any bitwise operation, the operands are best placed as follows:
0 1 0 1 // 5 0 1 1 0 // 6
And then apply the operation to each column of bits individually. As you remember, logical OR returns true (1) if one or both of its operands are true (1). Bitwise OR works in a similar way . Expression 5 | 6 is processed as follows:
0 1 0 1 // 5 0 1 1 0 // 6 ——- 0 1 1 1 // 7
Result:
0111 (binary) = 7 (decimal)
You can also process complex OR expressions, for example, 1 | 4 | 6. If at least one bit in a column is 1, then the result of the entire column is 1. For example:
0 0 0 1 // 1 0 1 0 0 // 4 0 1 1 0 // 6 ——— 0 1 1 1 // 7
Result 1 | 4 | 6 is decimal 7.
Bitwise AND works similarly to logical AND - it returns true only if both bits in the column are 1. Consider the expression 5 & 6:
0 1 0 1 // 5 0 1 1 0 // 6 ——— 0 1 0 0 // 4
You can also solve complex AND expressions, for example, 1 & 3 & 7. Only if all the bits in the column are 1, the result of the column will be 1.
0 0 0 1 // 1 0 0 1 1 // 3 0 1 1 1 // 7 ——— 0 0 0 1 // 1
The last operator is the bitwise exclusive OR (^) (abbreviated “XOR” from the English “e X exclusive OR ”). When processing two operands, XOR returns true (1) only if one and only one of the operands is true (1). If there are none or all operands are 1, then the result will be false (0). Consider the expression 6^3:
0 1 1 0 // 6 0 0 1 1 // 3 ——- 0 1 0 1 // 5
You can also solve complex XOR expressions, for example, 1 ^ 3 ^ 7. If there is an even number of units in the column, then the result will be 0, but if there is an odd number, then the result will be 1. For example:
0 0 0 1 // 1 0 0 1 1 // 3 0 1 1 1 // 7 ——— 0 1 0 1 // 5
Clinical significance [edit | edit code ]
In clinical practice, the leukogram is of great importance, since with any changes in the body, the percentage of some types of white blood cells increases or decreases due to an increase or decrease to one degree or another in others. Based on leukogram data, one can judge the course of the pathological process, the occurrence of complications and predict the outcome of the disease. Leukogram data must be compared with the clinical manifestation of the disease
Description of specific indicators [ edit | edit code ]
Neutrophils [edit | edit code ]
Neutrophils
normally presented in three or two groups: may be present in small quantities or absent: young (u) 0-0.5%; rod-nuclear (s/i) 1-5% and segmented (s/i) 40-68%. They have mainly bactericidal and detoxification functions, bearing the conventional name of microphages (which reflects the leading mechanism of their immune function - phagocytosis).
Depending on the degree of maturity and the shape of the nucleus, band (younger) and segmented (mature) neutrophils are distinguished in the peripheral blood. Younger cells of the neutrophil series - young (metamyelocytes), myelocytes, promyelocytes - appear in the peripheral blood in case of pathology and are evidence of stimulation of the formation of cells of this type. The duration of neutrophil circulation in the blood is on average approximately 6.5 hours, then they migrate into tissues.
Normal blood content: 48-78%
Limits of the normal content of neutrophils in the leukocyte formula:
In children, 2 crossovers of the leukocyte formula normally occur at the age of five days and 4-5 years, while up to 5 days neutrophils predominate over lymphocytes, almost like in an adult, then the first crossover occurs: the ratio of lymphocytes/neutrophils is approximately 20%/60%. turns into 60%/20%, this remains until the second crossover of the leukocyte formula, usually it occurs at 4 years, but is acceptable up to 5 years, after which the content and proportions of neutrophils/lymphocytes correspond to the norms of an adult.
- inflammatory processes;
- myocardial infarction, lung;
- malignant neoplasms;
- many infectious processes.
Lead to a decrease (neutropenia)
- viral infections (hepatitis, measles, rubella, influenza, chicken pox, polio);
- infections caused by protozoa (toxoplasma, malaria);
- post-infectious conditions;
- aplastic anemia;
- fungal infections;
- chronic bacterial infections (strepto- or staphylococcal, tuberculosis, brucellosis);
- carrying out radiation therapy.
Increased number of immature neutrophils (shift to the left):
- acute inflammatory processes (lobar pneumonia);
- some infectious diseases (scarlet fever, erysipelas, diphtheria);
- malignant tumors (cancer of the kidney parenchyma, mammary and prostate glands) and metastasis to the bone marrow;
- myeloproliferative diseases, especially chronic myeloid leukemia;
- tuberculosis;
- myocardial infarction;
- bleeding;
- hemolytic crisis;
- sepsis;
- intoxication;
- shock;
- physical stress;
- acidosis and coma.
Eosinophils [edit | edit code ]
Eosinophils
(E) - also have phagocytic properties, but this property is used primarily to participate in the allergic process. They phagocytose the antigen-antibody complex formed predominantly by Ig E.
An increase (eosinophilia) is observed when
- allergic conditions (bronchial asthma, allergic skin lesions, hay fever);
- helminthic infestation (ascariasis, echinococcosis, giardiasis, trichinosis, strongyloidiasis);
- infectious diseases (in the recovery stage);
- after administration of antibiotics;
- collagenoses.
A decrease (eosinopenia) occurs when
- some acute infectious diseases (typhoid fever, dysentery);
- acute appendicitis;
- sepsis;
- injuries;
- burns;
- surgical interventions;
- on the first day of myocardial infarction.
Basophils [edit | edit code ]
Basophils
(B) - participate in inflammatory and allergic processes in the body.
An increase in basophils occurs when
- allergic conditions;
- diseases of the blood system;
- acute inflammatory processes in the liver;
- endocrine disorders;
- chronic inflammation in the gastrointestinal tract;
- ulcerative inflammation of the intestines;
- lymphogranulomatosis.
A decrease in basophils (basopenia) occurs when
- long-term radiation therapy;
- acute infections;
- acute pneumonia;
- hyperfunction of the thyroid gland;
- stressful conditions.
Monocytes [edit | edit code ]
Monocytes
(M) - belong to agranulocytes. They belong to the system of phagocytic mononuclear cells. They remove dying cells, debris from destroyed cells, denatured protein, bacteria and antigen-antibody complexes from the body.
Normal monocyte content in the blood: 3-11%
- for infectious diseases (tuberculosis, syphilis, protozoal infections);
- for some diseases of the blood system;
- for malignant neoplasms;
- for collagenosis;
- during surgical interventions;
- during the recovery period after acute conditions.
Bitwise assignment operators
As with arithmetic assignment operators, C++ provides bitwise assignment operators to make it easier to make changes to variables.
| Operator | Symbol | Example | Operation |
| Bitwise left shift assignment | <<= | x <<= y | Shift the bits in x to the left by y bits |
| Bitwise right shift assignment | >>= | x >>= y | Shift the bits in x to the right by y bits |
| Assignment with bitwise OR operation | |= | x |= y | Assigning the result of the expression x | y variable x |
| Assignment with bitwise AND operation | &= | x &= y | Assigning the result of the expression x & y to the variable x |
| Assignment with bitwise exclusive OR operation | ^= | x^=y | Assigning the result of the expression x^y to a variable x |
For example, instead of x = x << 1; we can write x <<= 1;.
Who needs a blood test: alarming symptoms
The increase in the neutrophil fraction does not go away without a trace. Most of the changes that occur in this case have pronounced signs (weakness, dizziness, decreased performance and blood pressure), if they appear, you should consult a doctor. This is necessary in order to timely determine the causes of changes in blood composition. Checking the level of all white blood fractions is required in the following cases:
- suspected infection or inflammation;
- exacerbation of chronic pathology;
- to assess the effectiveness of prescribed treatment;
- causeless weight loss;
- acute abdominal pain;
- swelling of the lymph nodes;
- during preventive examinations.
For a leukogram, blood is taken from a finger or from a vein in the morning, on an empty stomach. For 7-10 days, you should stop taking medications that change the composition of the blood (oral contraceptives, psychostimulants, NSAIDs, allopurinol). Also, you should not drink alcohol or food that is difficult to digest, do not smoke, do not lift weights, and avoid excessive physical activity - any of these factors will shift the result with an error.
Lymphocytes
Lymphocytes are the main cells that provide our immunity and regulate the number and activity of other blood cells. They come in three types:
- natural, or natural killers (controlling the timely death of “broken” and old cells);
- T-lymphocytes – provide the cellular component of immunity;
- B lymphocytes are responsible for the production of immunoglobulins.
An adult should normally have at least 19% lymphocytes in the peripheral blood, but no more than 37. In children, this figure is higher - up to 50. An increase in the number of cells can be both physiological and pathological. A natural rise in the level of lymphocytes occurs after heavy physical labor, and in women at the beginning of the menstrual cycle. An excessive number of these cells indicates the presence of a viral infectious disease.
A decrease in lymphocytes is possible in immunodeficiency states, taking adrenal hormones, malignant oncological processes, peripheral circulatory failure, as a rule, at the same time there is a shift in the leukocyte formula to the left. An example of such a condition is a severe viral or bacterial infection.
Age norm
A shift of the leukocyte formula to the left is a fairly general concept, depending on the basic indicators, the specifics of the disease, as well as age, since the absolute number of leukocytes changes depending on the period of a person’s life.
In the first year, the norm of white blood cells is from 6 to 17 thousand leukocytes in one microliter of blood. By four years, this level drops to 15.5 thousand. At six years the figure drops by another thousand. Over the next 4 years, the number of leukocytes slowly decreases to 4.5-13 thousand per microliter. When a child enters puberty, the level of white cells approaches that of an adult and a physiological increase is no longer observed, except perhaps only in certain fractions.
How to determine the shift in the leukocyte formula? To do this, it is necessary to divide the absolute number of leukocytes first into granulocytes and agranulocytes, then differentiate among granulocytes into neutrophils, eosinophils and basophils, and then count how many young cells among neutrophils and how many mature ones. If young neutrophils predominate, then there is a shift. To make this process easier, there are special techniques and indices.